Batch Norm, Layer Norm, Instance Norm, Group Norm

自 Batch Normalization 从 2015 年被 Google 提出来之后，又诞生了很多 Normalization 方法，如 Layer Normalization, Instance Normalization, Group Normalization。 这些方法作用、效果各不相同，但却有着统一的内核和本质：计算输入数据在某些维度上的方差和均值，归一化，最后用可学习参数映射归一化后的特征。这可以统一表达为：

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

我们以图像数据为例子，给定输入数据 $x \in (N, C, H, W)$, 其中 $N, C, H, W$ 分别为 batch size, 通道数，图像高和宽。

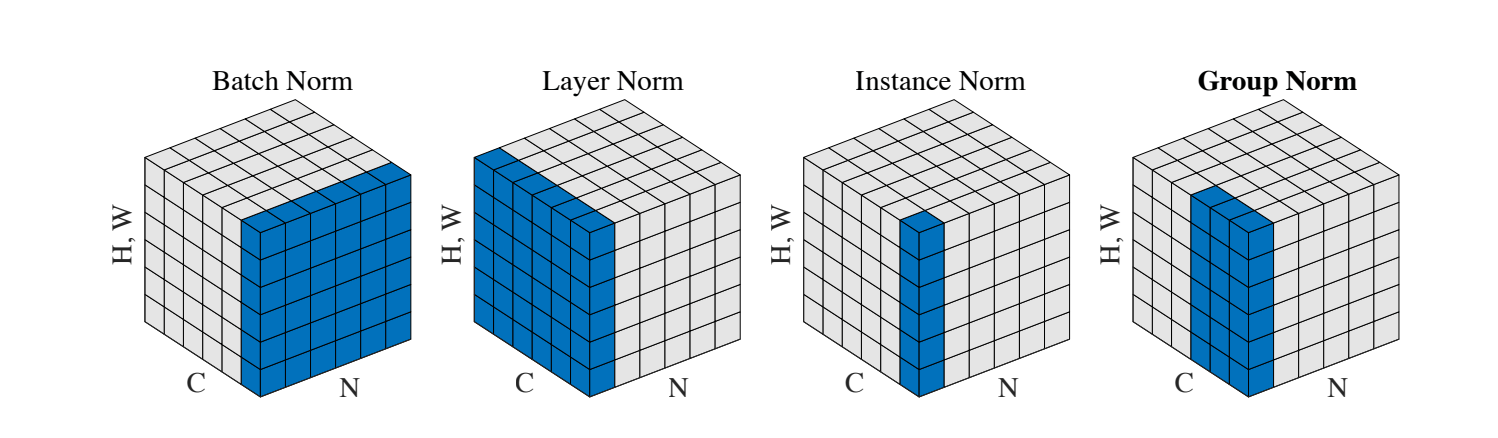
如上图所示，BN 计算在 $N, H, W$ 维度上的均值方差，LN 计算在 $C, H, W$ 维度上的均值方差，IN 计算在 $H, W$ 维度上的均值方差，GN 计算在 $C’, H, W$ 维度上的均值方差，其中 $C’$ 是分组后的通道个数。

计算维度的不同是这些方法的唯一区别。也正是因为计算维度的不同，也导致了不同的效果和特性。

• BN 计算依赖 $N, H, W$，因此当 batch size 较小时效果可能并不理想，且 batch size 对结果影响较大。
• IN 计算依赖 $H, W$，不依赖 batch size, 相当于计算每个单独的 instance 不同通道的特征，IN 也因此常用于风格转换。
• LN 计算依赖 $C, H, W$，舍弃了对 batch size 的依赖，因此常用在 batch size 变化的模型中，如 RNN。另外 LN 与 BN 和 IN 不同的是，BN 和 IN 整个通道用的是同一个标量进行映射，而 LN 通道内每一个元素都采用不同的标量进行映射。因此前者可学习参数的形状为 $(C)$, 而 LN 可学习参数的形状为 $(C \times H \times W)$。
• GN 首先将通道分组 $(N, C, H, W) \rightarrow (N, G, C’, H, W)$（其中$C’ = \frac{C}{G}$），计算依赖 $C’, H, W$, 显然不依赖 batch size。而将特征分组，有点类似将类似特征归一化（比形状、亮度和纹理等），实验证明 GN 效果很好。而且事实上，GN 可以看作是 IN 和 LN 的中间体：当分组个数等于 1 时相当于不分组，是计算 $C, H, W$ 上的均值方差，而当分组个数等于通道个数时（$G = C$），相当于计算在 $H, W$ 上的均值方差，于是退化成了 IN。

我们可以很轻松的用 PyTorch 实现每个方法的等效版本：

BN

inputs = torch.randn(5, 256, 32, 32)  # (N, C, H, W)
bn = nn.BatchNorm2d(256)  # Weight shape: (C, )

# weight default is 1
bn.weight.data = torch.rand_like(bn.weight)

# compute on (N, H, W)
var, mean = torch.var_mean(inputs, dim=(0, 2, 3), keepdim=True, unbiased=False)  # (1, C, 1, 1)
std = (var + bn.eps).sqrt()  # (1, C, 1, 1)
norm = (inputs - mean) / std  # (N, C, H, W)

print(torch.allclose(
    norm * bn.weight.view(1, 256, 1, 1) + bn.bias.view(1, 256, 1, 1),
    bn(inputs))
)  # True

IN

inputs = torch.randn(5, 256, 32, 32)  # (N, C, H, W)
ins = nn.InstanceNorm2d(256, affine=True)  # Weight shape: (C, )

# weight default is 1
ins.weight.data = torch.rand_like(ins.weight)

# compute on (H, W)
var, mean = torch.var_mean(inputs, dim=(2, 3), keepdim=True, unbiased=False)  # (N, C, 1, 1)
std = (var + ins.eps).sqrt()  # (N, C, 1, 1)
norm = (inputs - mean) / std  # (N, C, H, W)

print(torch.allclose(
    norm * ins.weight.view(1, 256, 1, 1) + ins.bias.view(1, 256, 1, 1),
    ins(inputs))
)  # True

LN

inputs = torch.randn(5, 256, 32, 32)  # (N, C, H, W)
normalized_shape = inputs.shape[1:]  # Normalize on (C, H, W)
ln = nn.LayerNorm(normalized_shape)

# weight default is 1
ln.weight.data = torch.rand_like(ln.weight)

# compute on (C, H, W)
var, mean = torch.var_mean(inputs, dim=(1, 2, 3), keepdim=True, unbiased=False)  # (N, 1, 1, 1)
std = (var + ln.eps).sqrt()  # (N, 1, 1, 1)
norm = (inputs - mean) / std  # (N, C, H, W)

print(torch.allclose(norm * ln.weight + ln.bias, ln(inputs)))  # True

GN

inputs = torch.randn(5, 256, 32, 32)  # (N, C, H, W)
num_groups = 32
bn = nn.GroupNorm(num_groups=num_groups, num_channels=256)  # Weight shape: (C, )

# weight default is 1
bn.weight.data = torch.rand_like(bn.weight)

grouped_inputs = inputs.view(5, num_groups, 256 // num_groups, 32, 32)  # (N, G, C', H, W)

# compute on (C', H, W)
var, mean = torch.var_mean(grouped_inputs, dim=(2, 3, 4), keepdim=True, unbiased=False)  # (N, G, 1, 1, 1)
std = (var + bn.eps).sqrt()  # # (N, G, 1, 1, 1)
norm = (grouped_inputs - mean) / std  # (N, G, C', H, W)

print(torch.allclose(
    norm.view(5, 256, 32, 32) * bn.weight.view(1, 256, 1, 1) + bn.bias.view(1, 256, 1, 1),
    bn(inputs))
)  # True