堆排序以及最大优先队列
堆排序(heapsort)是一种比较快速的排序方式,它的时间复杂度为O(nlgn),而且堆排序具有空间原址性:即任何时候只需要有限(常数个)的空间来存储临时数据。而且堆排序还被应用在构造优先级队列中,本文将会用Java实现一个最大堆,并利用最大堆实现优先级队列。
最大堆的性质
- 是一棵近似的完全二叉树,除了最底层,其它是全满,且从左向右填充。
- 树的每个节点对应数组一个元素,根节点对应数组下标
0元素。 - 对于下标
i,它的父节点下标为(i + 1) / 2 - 1,左孩子节点下标为i * 2 + 1,右孩子节点下标为i * 2 + 2。 - 最大堆中,每个结点都必须大于等于左右孩子节点。
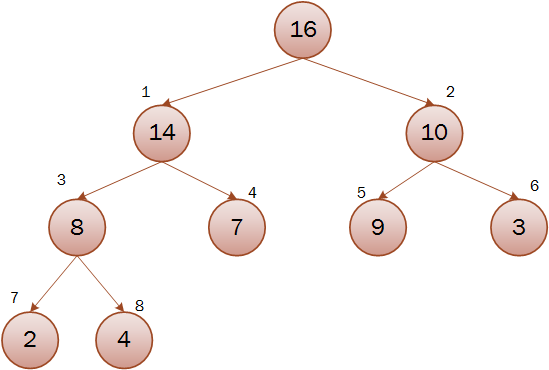

堆排序
1.维护最大堆
为了建立一个最大堆,我们需要设计一个算法来维护最大堆的性质。对于节点i,我们假设它们的左右子树都是最大堆,而节点i因为小于左右孩子而违背了最大堆的性质,因此我们需要对节点i进行逐级下降,从而使得以节点i为根结点的子树满足最大堆的性质。
private void maxHeapify(int[] a, int i, int length) {
int l = left(i);
int r = right(i);
int max;
if (l < length && a[l] > a[i]) {
max = l;
} else {
max = i;
}
if (r < length && a[r] > a[max]) {
max = r;
}
if (max != i) {
swap(a, i, max);
maxHeapify(a, max, length);
}
}
上述代码的解释是:
对于节点i(即数组下标i),首先获取它的左右子孩子下标,分别存储到l,r变量中,其中left和right函数可以根据最大堆的性质得到,如下:
private int left(int i) {
return i * 2 + 1;
}
private int right(int i) {
return i * 2 + 2;
}
变量length是要维护的数组的长度,它的值<=数组的真实长度。临时变量max用来存储节点i,左孩子和右孩子这三者最大者的下标。因此,首先比较左孩子a[l]是否大于节点i,是的话将左孩子下标l赋值给max,否则,当前最大者仍为节点i,并把i的值赋给max。然后当前最大者和右孩子比较,小于右孩子的话就把下标r赋值给max。到目前为止,我们找到了节点i,左孩子和右孩子这三者之中的最大者的下标max,如果节点i本来就是最大的,那么就不需要维护了,所以函数结束。否则的话,有孩子节点大于节点i,因此我们需要将节点i和较大的那个孩子进行交换,即swap(a, i, max),swap函数如下:
private void swap(int[] a, int i, int j) {
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
交换之后,节点max的值变成了较小的原来节点i的值,因此,以节点max为根节点的子树可能违背最大堆的性质。注意到此时问题和一开始一模一样,只是节点i变成了节点max,因此递归调用maxHeapify(a, max, length)即可。
如果把第一张图的节点1的值改为1,这时从节点1开始调用maxHeapify(a, 1, a.length,整个流程如下:
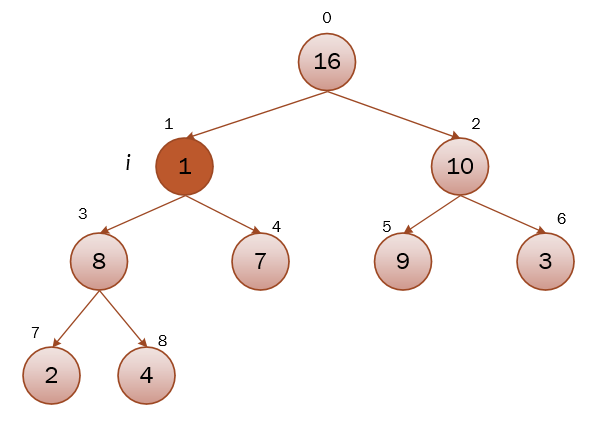
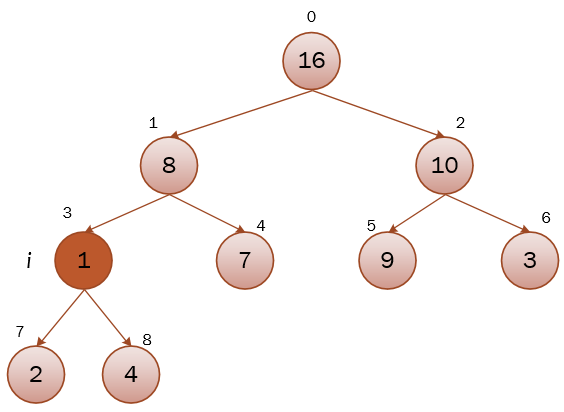
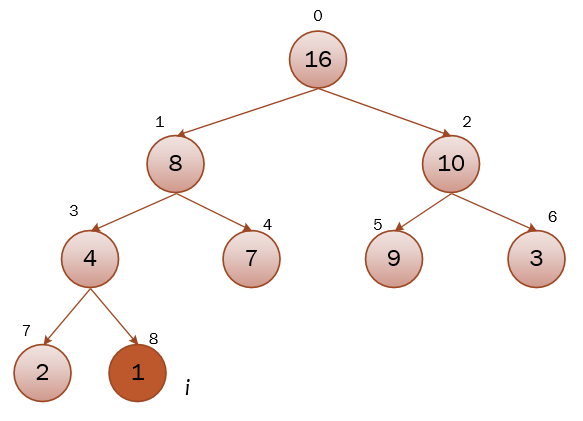
可以看到,在经历两次递归调用,逐级下沉,原来因为1节点变小,而被打破的最大堆,又重新维护完成。
2.建立最大堆
我们采用自底向上的方法来建立一个最大堆。通过观察发现,下标为a.length / 2 到a.length - 1的节点均为叶子节点,没有子孩子。这意味着,它们已经是一个最大堆,只是仅有一个元素。因此,我们只需要自底向上,对其他节点调用maxHeapify来维护最大堆即可:
private void buildMaxHeap(int a[]) {
for (int i = a.length / 2 + 1; i >= 0; i--) {
maxHeapify(a, i);
}
}
注意,循环变量从a.length / 2 + 1开始,因为a.length / 2 到a.length - 1的节点满足最大堆,即a.length / 2 + 1的左右子孩子(如果有的话)是最大堆,符合使用maxHeapify调用条件。如果我们对数组[10, 8, 11, 8, 14, 9, 4, 1, 17]进行建立最大堆,那么输出数组为[17, 14, 11, 8, 10, 9, 4, 1, 8]:
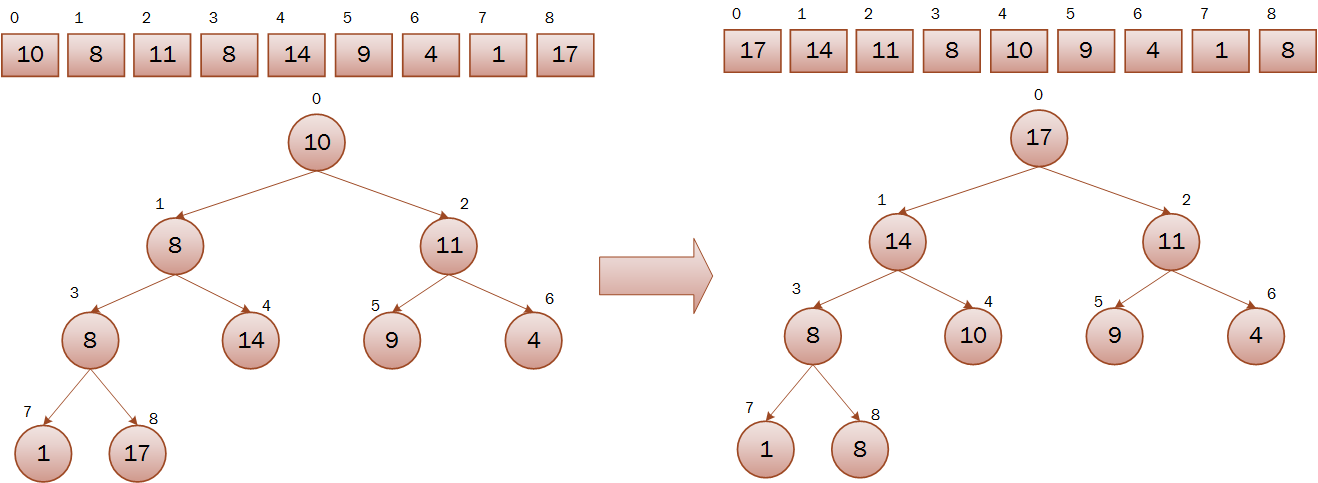

3.堆排序
在第二步建立完成最大堆之后,注意到整个数组的** 最大元素 总是在最大堆的第一个,即a[0]。这时,如果我们拿走第一个元素,放到数组的最后一个位置,然后对第一个元素进行维护最大堆maxHeapify,如此循环进行,便可完成整个数组的排序**。
public void heapSort(int[] a) {
buildMaxHeap(a);//首先建立最大堆,完成后第一个元素为最大值
int length = a.length;
for (int i = a.length - 1; i >= 1; i--) {
swap(a, i, 0);//将第一个最大的元素移到后面,并且在maxHeapify的过程中通过减小length忽略它
length--;
maxHeapify(a, 0, length);
}
}
这样我们就完成了对数组的从小到大排序。
最大优先队列
堆排序是一个优秀的算法,在操作系统中可以利用最大堆实现最大优先队列来实现共享计算机系统的作业调度。最大优先队列记录各个作业之间的相对优先级,当某个作业中断后选出具有最高优先级的队列来执行。最大优先级队列应该支持如下操作:
maximum():返回堆的最大值。extractMax():返回堆的最大值并从堆中删除。heapIncreaseKey(i, key):将下标为i的元素增大为key。maxHeapInsert(key):将元素key插入到堆中。
maximum()最简单,直接返回第一个元素:
public int maximum() {
return a[0];
}
extractMax也很简单,取出第一个后,只需把最后一个元素放到第一个,然后对第一个元素进行维护最大堆即可:
public int extractMax() {
int max = a[0];
a[0] = a[a.length - 1];
int[] newA = new int[a.length - 1];
System.arraycopy(a, 0, newA, 0, newA.length);
maxHeapify(newA, 0, newA.length);
return max;
}

heapIncreaseKey(i, key)会增大下标为i的元素为key。首先将a[i]的值更新为key,因为增大的a[i]关键字可能会违背最大堆的性质,因此我们需要对a[i]进行逐级上升。即将当前元素逐级与父节点比较,如果大于父节点,则与父节点进行交换,一直到当前元素小于父节点为止:
public void heapIncreaseKey(int i, int key) {
if (key > a[i]) {
a[i] = key;
while (i > 0 && a[parent(i)] < a[i]) { //逐级上升
swap(a, parent(i), i);
i = parent(i);
}
} else {
throw new IllegalArgumentException("key is too small");
}
}
private int parent(int i) {
return (i + 1) / 2 - 1;
}
maxHeapInsert(key)十分简单,因为它等价于数组长度增加一,然后最后一个元素设置为-∞,然后把它增大为key的操作:
public void maxHeapInsert(int key) {
int[] newA = new int[a.length + 1];
System.arraycopy(a, 0, newA, 0, a.length);
newA[newA.length - 1] = Integer.MIN_VALUE;
this.a = newA;
heapIncreaseKey(a.length - 1, key);
}
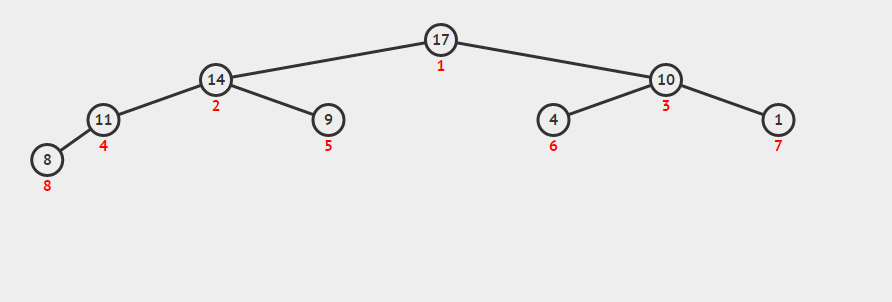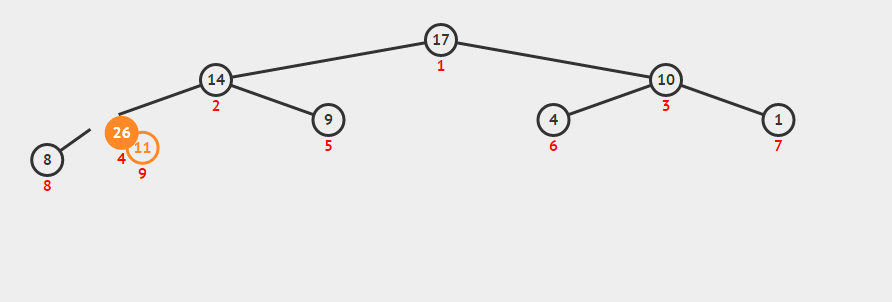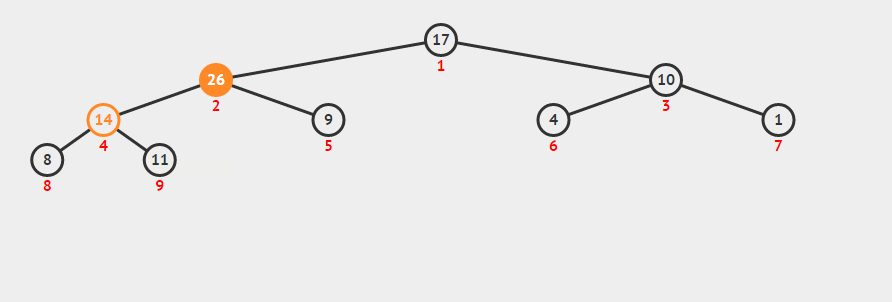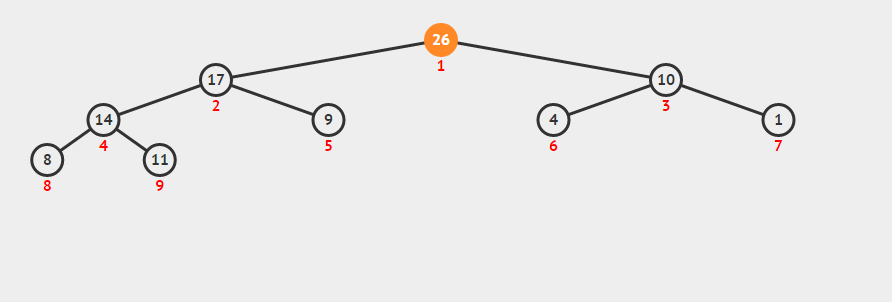
在一个包含n个元素的堆中,所有优先级队列的操作都可以在O(lgn)的时间内完成。
源代码可以在这里找到:lufficc/Algorithm
文章来自自己的理解以及算法导论。