循环神经网络（Recurrent Neural Network）简介

我们人类理解事物都是基于上下文的，一句话只有在明确的上下文中才能有确定含义。

而传统的神经网络不能实现，因为神经网络是一对一的，我们输入一个 input，网络输出一个 output，而多个 input 之间却没有联系。就好比我们我们输入一部电影的一帧，让它预测接下来将会发生什么，显然没有先前剧情的支撑神经网络不可能做出好的预测。

RNN

Recurrent neural networks 正是为了解决此类问题诞生的。RNN 网络连接中存在循环，并且能够存储信息。

Recurrent neural network

上图就是一个 RNN，输入 xt，得到 ht。区别在于 A 存在循环，允许将上一步的结果传递给下一步。如果不考虑循环，和普通的神经网络没有区别，都是给予输入，得到输出。但是循环的存在，可以让上次的运算结果传递给下一次使用，这样在携带了上次的“记忆”之后，本次运算会在上次的运算基础上做出更好地预测。如果我们把每一步展开来看，会更简单：

file

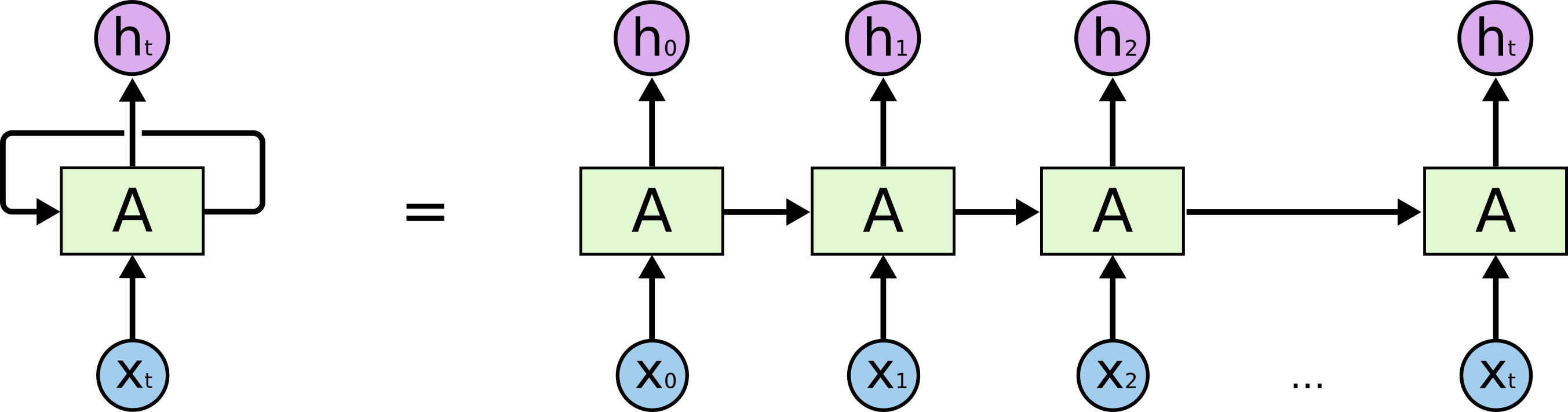
上图每一次运算都是一个时间步，一共进行了 t 个时间步。每一个时间步输入 xt，得到输出 ht 。因为循环的存在，ht 的运算结果与 x0 – xt 相关。这 t 个时间步称为一个完整的序列（Sequence），也可以称为训练数据集中的一个样本。举个例子，假设我们要用一句话预测某个结果，那么完整的这句话就是一个序列，每个词就是输入xt。

将其用更公式化的方式表示就是：

file

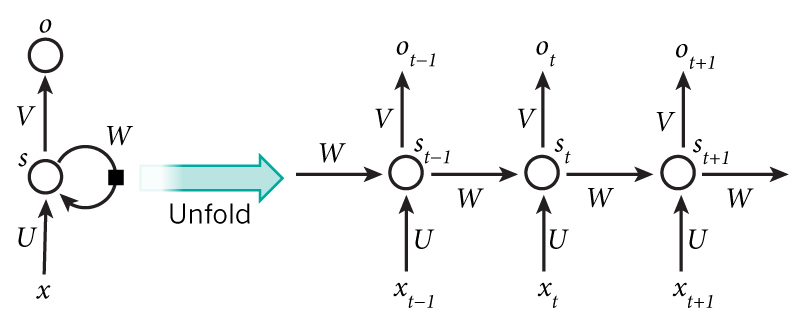
xt ：时间步 t 的输入向量，如 x1 可以是代表一句话（一个序列）第二个单词的 One-Hot 向量。
st：时间步 t 的输入向量 RNN 的隐藏状态（hidden state），即网络的记忆。st 计算依赖于上一个状态 st-1 和当前输入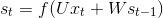：。f 为非线性激活函数如 tanh 和 ReLU。
ot（即上上图的 ht）：时间步 t 的输出，。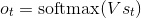

这些本质上就是一些矩阵的运算，具体介绍和实现可以看这里。

注意上图我们每一个时间步都会得到一个输出ht （ot）。但实际情况我们可能会舍弃某些输出，只取我们感兴趣的部分。大概可以分为以下几类：

file

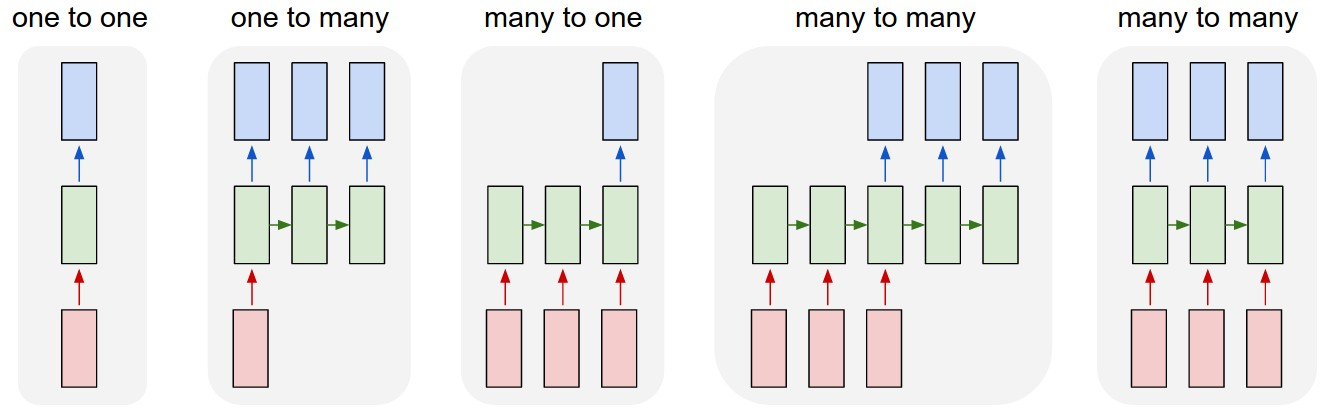
是没有采用 RNN 的情形。如图像分类。
输入一个，输出一个序列（保留每个时间步的结果）。如输入一张图片，输出对这张图片的描述（Sequence）。
输入序列，只取最后一个时间步的结果。如输入一句话，来判断这句话的情感是消极的还是积极的，显然最后一个时间步结果最可靠，因为每个单词都进行了考虑。再比如，把一张图片看成序列，对图片分类，后面的例子就是用的这种。
输入序列，输出序列。如机器翻译，很好理解。
同步的（Synced ）序列输入和序列输出。如给视频的每一帧标上标签。

注意，每一个时间步的长度不一定固定，理论上我们可以“无限向右扩展”。 RNN 已经取得了很多成果：翻译，语音识别，语言建模，描述图片等，但普通的 RNN 很难训练，因为存在 梯度消失 和 梯度爆炸 等问题。而 RNN 的变体，LSTM 正是为了解决此类问题诞生的。

LSTM

LSTM，全称为长短期记忆网络(Long Short Term Memory Networks)，是一种特殊的RNN，能够学习到长期依赖关系。LSTM由Hochreiter & Schmidhuber (1997)提出，许多研究者进行了一系列的工作对其改进并使之发扬光大。LSTM在许多问题上效果非常好，现在被广泛使用。

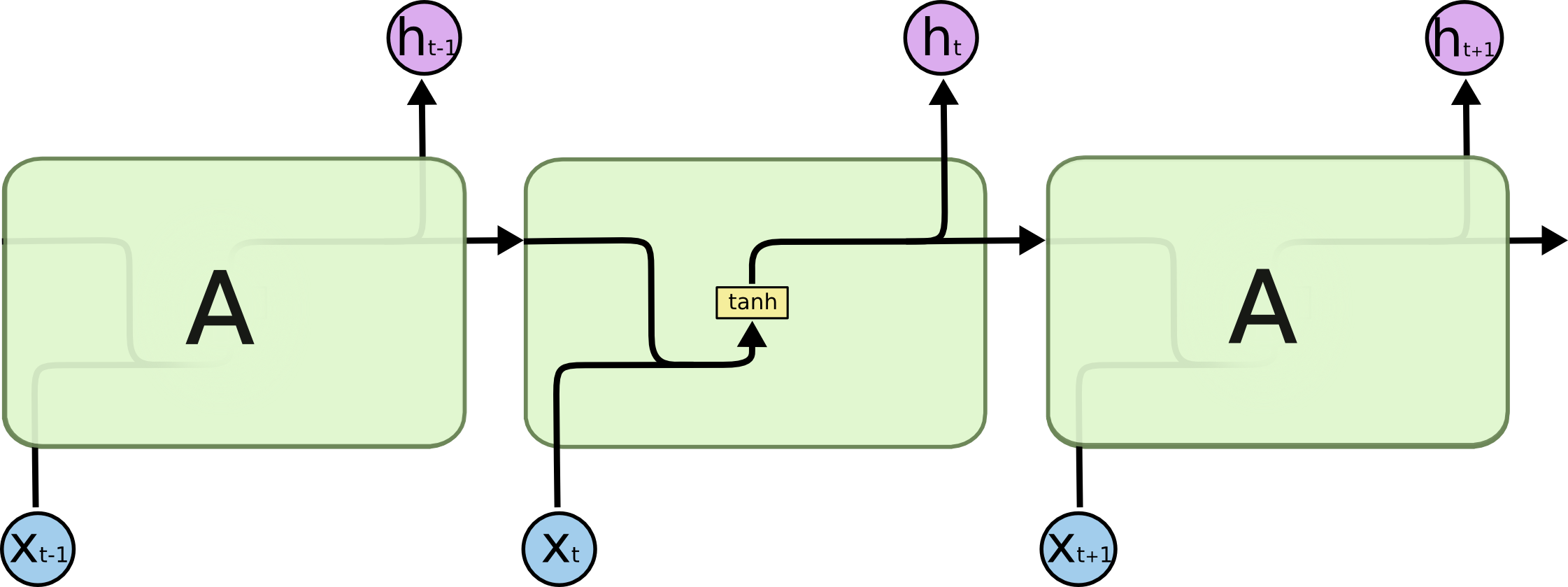
普通 RNN 于 LSTM 的区别在于，RNN 只有一层（如单个tanh 层）：

file

LSTM 的整体结构（链式）与 RNN 一致，但 LSTM 内部有四层，并用一定的方式组织：

file

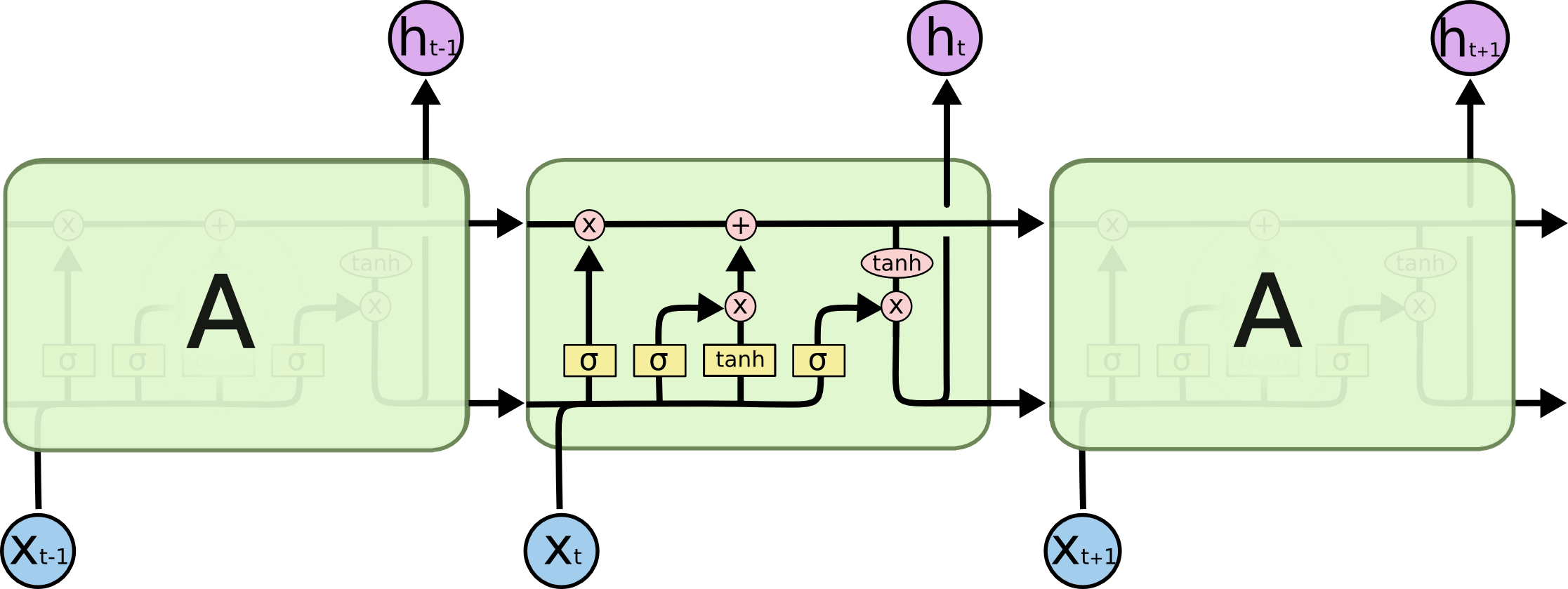
关于这四层的解释，Understanding LSTM Networks 已经完美阐述了，这里只说我的理解吧。

LSTM 与普通 RNN 的整体结构一样，都是输入 xt，输出 ot，传递给下一步 st。区别在于 st 的计算。普通 RNN st 的计算简单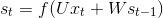，而 LSTM 为了解决长期依赖关系，引入了三个“门”：Input, forget and output gates，因此计算也变得稍微复杂：

file

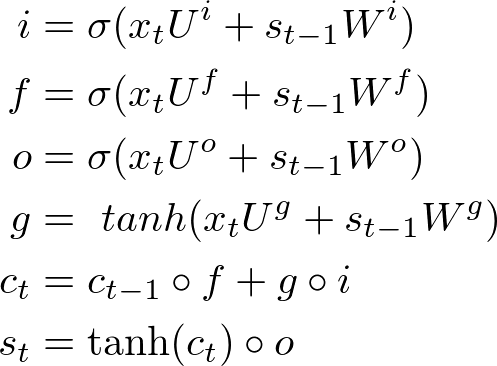
虽然六个公式看起来复杂，但是 i，f，o（即 input, forget and output gates）的计算公式是一样的，都是只与当前输入和上一状态有关，只是所用的参数不同。而 g 叫做 “候选隐藏状态”，因为 g 和普通 RNN 的隐藏状态 st 计算方法一样。为什么时候选的呢？关键在于 ct 。ct 就是 LSTM 的“内部记忆”（Internal Memory），ct 计算公式很有意思： ct-1 乘以 f 加上 g 乘以 i （这里的乘法不是矩阵相乘，而是Pointwise Operation，即元素对应相乘），即忘掉 ct-1 中应该忘掉的，输入 g 中应该输入的。这就是 input gate 和 forget gate 的来历。试想 f 全为 0，相当于完全忘记 ct-1； i 全为1，相当于取 g 的所有作为 ct。因为 f 和 i 通常由 sigmod 函数获得，因此介于 0~1，即这两个极端之间。所以最后 st 的计算，就是tanh(ct) 乘以（Pointwise Operation）o，只取值得输出的。因此，这些公式没那么复杂，input, forget and output gates 就是为了对 st 的计算加以限制，忘掉无用的久远的记忆，过滤输入中有价值的，输出我们想要的结果。

整个解释，这一个图完美概括了：

file

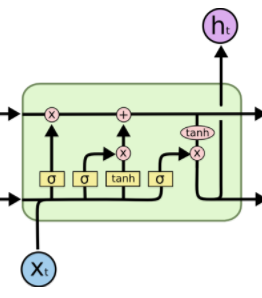
所以，一定要看Understanding LSTM Networks。

用 LSTM 实现分类任务

RNN 解决了序列的依赖问题，如果我们把图片看成一个序列能对其完成分类吗？答案是肯定的。一张图片就是一个完整的序列，我们只取最后一个时间步的输出作为分类结果即可。

以 MNIST 数据集为例，MNIST 一张图片大小为 28 x 28，把每一行像素看作输入 xt，一共有 28 行，即 28 个时间步，正好一张图片就是一个完整的序列。

import tensorflow as tf
from tensorflow.contrib import rnn

# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("data/", one_hot=True)

lr = 0.001
training_iters = 100000
batch_size = 128
display_step = 10

n_input = 28
n_step = 28
n_hidden = 128
n_classes = 10

x = tf.placeholder(tf.float32, [None, n_step, n_input])
y = tf.placeholder(tf.float32, [None, n_classes])
w = tf.Variable(tf.random_normal([n_hidden, n_classes]))
b = tf.Variable(tf.random_normal([n_classes]))


def RNN(x):
    # x (batch, n_step, n_input)
    # x = tf.unstack(x, n_step, 1)
    cell = rnn.BasicLSTMCell(n_hidden)

    # static_rnn
    # outputs: (n_step, batch, n_hidden)
    # state[0]: (batch, n_hidden), state is a tuple
    # outputs, state = rnn.static_rnn(cell, x, dtype=tf.float32)
    # -------------------------------------------------------
    # outputs: (batch, n_step, n_hidden)
    outputs, states = tf.nn.dynamic_rnn(cell, x, dtype=tf.float32)

    return tf.matmul(tf.transpose(outputs, [1, 0, 2])[-1], w) + b


pred = RNN(x)

cost = tf.reduce_mean(
    tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))

optimizer = tf.train.AdamOptimizer(lr).minimize(cost)
correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

tf.summary.scalar('accuracy', accuracy)
tf.summary.scalar('loss', cost)
summaries = tf.summary.merge_all()

with tf.Session() as sess:
    train_writer = tf.summary.FileWriter('logs/', sess.graph)
    init = tf.global_variables_initializer()
    sess.run(init)
    step = 1
    while batch_size * step < training_iters:
        batch_x, batch_y = mnist.train.next_batch(batch_size)
        batch_x = batch_x.reshape(batch_size, n_step, n_input)
        sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
        if step % display_step == 0:
            acc, loss = sess.run(
                [accuracy, cost], feed_dict={x: batch_x,
                                             y: batch_y})
            print("Iter " + str(step * batch_size) + ", Minibatch Loss= " + \
                  "{:.6f}".format(loss) + ", Training Accuracy= " + \
                  "{:.5f}".format(acc))
        if step % 100 == 0:
            s = sess.run(summaries, feed_dict={x: batch_x, y: batch_y})
            train_writer.add_summary(s, global_step=step)

        step += 1
    print("Optimization Finished!")

    test_len = 128
    test_data = mnist.test.images[:test_len].reshape((-1, n_step, n_input))
    test_label = mnist.test.labels[:test_len]
    print("Testing Accuracy:", \
          sess.run(accuracy, feed_dict={x: test_data, y: test_label}))

训练结果：

.............................................................
Iter 87040, Minibatch Loss= 0.107965, Training Accuracy= 0.96875
Iter 88320, Minibatch Loss= 0.169673, Training Accuracy= 0.96094
Iter 89600, Minibatch Loss= 0.115446, Training Accuracy= 0.96875
Iter 90880, Minibatch Loss= 0.106136, Training Accuracy= 0.96094
Iter 92160, Minibatch Loss= 0.199402, Training Accuracy= 0.96094
Iter 93440, Minibatch Loss= 0.061823, Training Accuracy= 0.98438
Iter 94720, Minibatch Loss= 0.132453, Training Accuracy= 0.95312
Iter 96000, Minibatch Loss= 0.044499, Training Accuracy= 1.00000
Iter 97280, Minibatch Loss= 0.161864, Training Accuracy= 0.94531
Iter 98560, Minibatch Loss= 0.114365, Training Accuracy= 0.95312
Iter 99840, Minibatch Loss= 0.127909, Training Accuracy= 0.96094
Optimization Finished!
Testing Accuracy: 0.992188

可以看到，取得了 0.992188 的准确率，训练时间也仅在 88 秒左右。

用 LSTM 实现回归任务

给定序列 sin(x)，求序列 cos(x)：

import tensorflow as tf
from tensorflow.contrib import rnn
import numpy as np
import matplotlib.pyplot as plt

BATCH_START = 0
TIME_STEPS = 20
BATCH_SIZE = 50
INPUT_SIZE = 1
OUTPUT_SIZE = 1
CELL_SIZE = 16
LR = 0.006


def get_batch():
    global BATCH_START, TIME_STEPS
    x = np.arange(BATCH_START, BATCH_START + BATCH_SIZE * TIME_STEPS).reshape(
        (BATCH_SIZE, TIME_STEPS)) / (10 * np.pi)

    sinx = np.sin(x)
    cosx = np.cos(x)

    BATCH_START += TIME_STEPS
    return sinx[:, :, np.newaxis], cosx[:, :, np.newaxis], x


class RNN():
    def __init__(self, x):
        cell = rnn.BasicLSTMCell(CELL_SIZE)
        self.cell_init_state = cell.zero_state(BATCH_SIZE, dtype=tf.float32)

        outputs, self.final_state = tf.nn.dynamic_rnn(
            cell, x, initial_state=self.cell_init_state, time_major=False)
        outputs = tf.reshape(outputs, (-1, CELL_SIZE))
        w = tf.Variable(tf.random_normal([CELL_SIZE, OUTPUT_SIZE]))
        b = tf.Variable(tf.random_normal([OUTPUT_SIZE]))
        self.pred = tf.matmul(outputs, w) + b


def ms_error(labels, logits):
    return tf.square(tf.subtract(labels, logits))


X = tf.placeholder(tf.float32, [None, TIME_STEPS, INPUT_SIZE])
Y = tf.placeholder(tf.float32, [None, TIME_STEPS, OUTPUT_SIZE])
rnn = RNN(X)
pred = rnn.pred

cost = tf.reduce_mean(
    tf.square(tf.subtract(tf.reshape(pred, [-1]), tf.reshape(Y, [-1]))))
optimizer = tf.train.AdamOptimizer(LR).minimize(cost)
correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
plt.figure(figsize=(10, 5))
plt.ion()
plt.show()
for i in range(200):
    sinx, cosx, x = get_batch()
    if i == 0:
        feed_dict = {
            X: sinx,
            Y: cosx,
        }
    else:
        feed_dict = {
            X: sinx,
            Y: cosx,
            rnn.cell_init_state: state,
        }
    _, state, outputs = sess.run(
        [optimizer, rnn.final_state, pred], feed_dict=feed_dict)

    plt.plot(x[0, :], cosx[0].flatten(), 'r', x[0, :],
             outputs.flatten()[:TIME_STEPS], 'b--')
    plt.ylim((-1.2, 1.2))
    plt.xlim(x[0, 0] - 10, x[0, -1])
    plt.draw()
    plt.pause(0.1)

    if i % 20 == 0:
        print('cost: ', sess.run(cost, feed_dict=feed_dict))

可以看到一开始并不能完整的拟合：

file

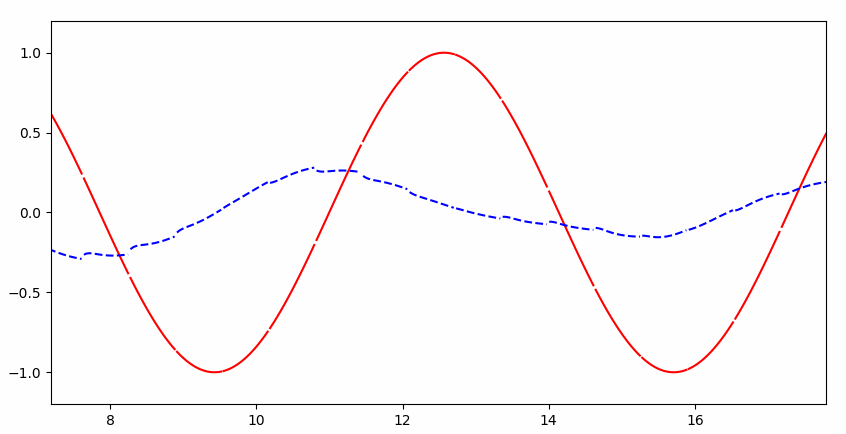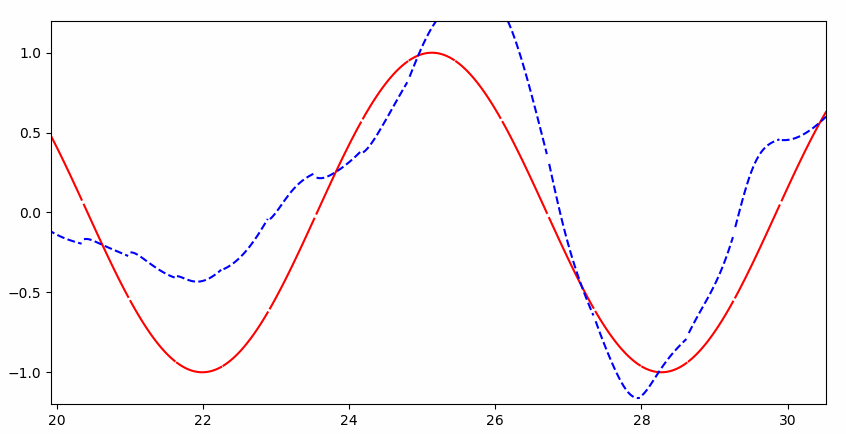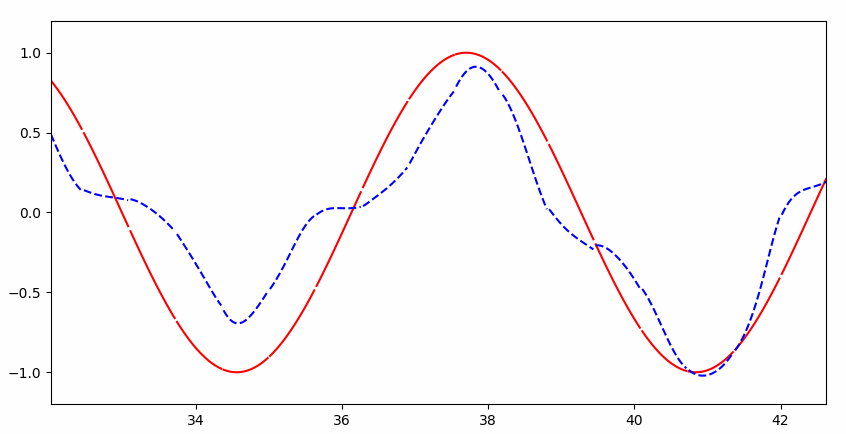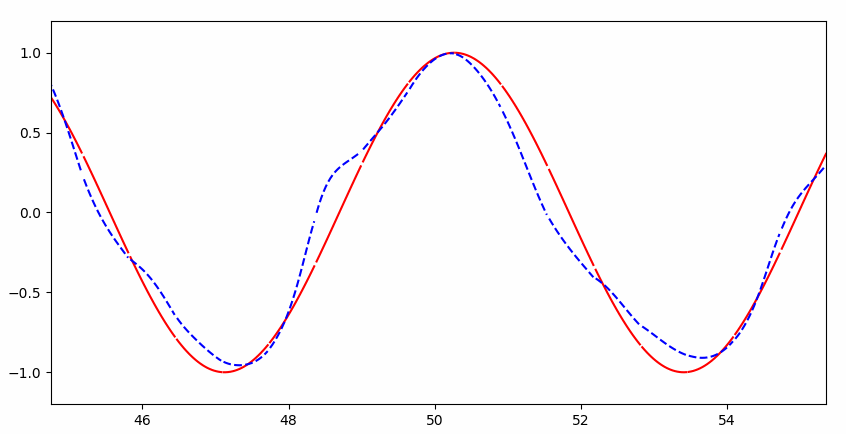
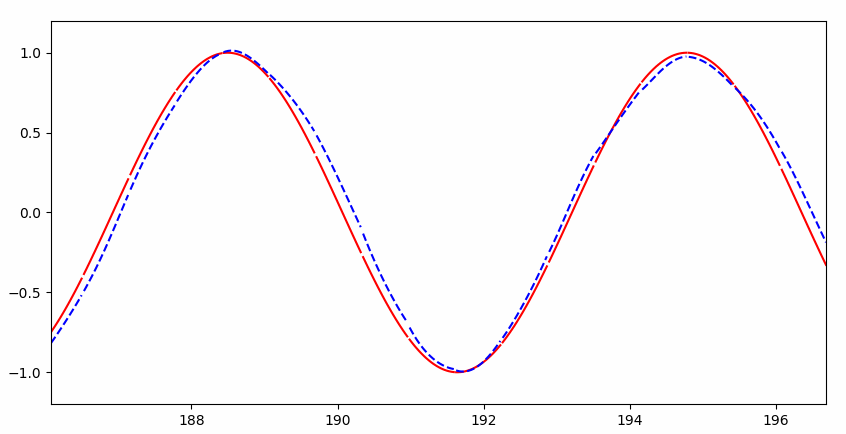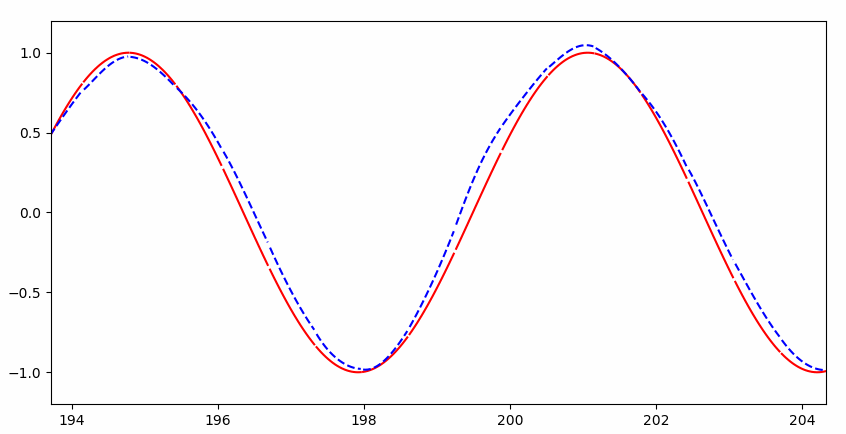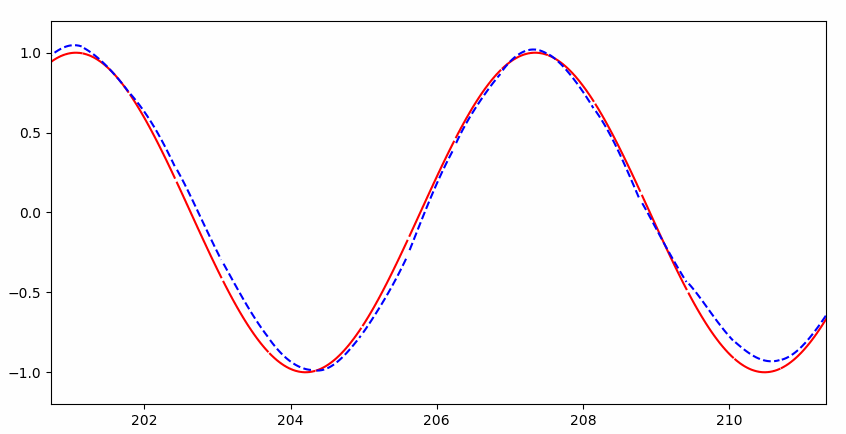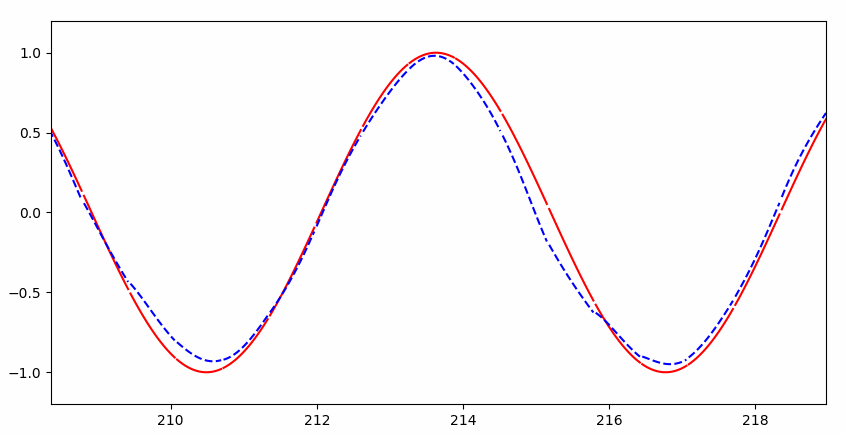
但是很快就几乎完美拟合：

file

RNN 与普通神经网络的直观区别

回到上个问题，我们给定序列 sin(x)，求序列 cos(x)，实际上是已知 cos(x) 的值，求 x 的值。大家都知道，已知 cos(x) 的值，可能会有两个 x 与之对应，进而 sin(x) 会有两个值（下图两个小黑点）：

file

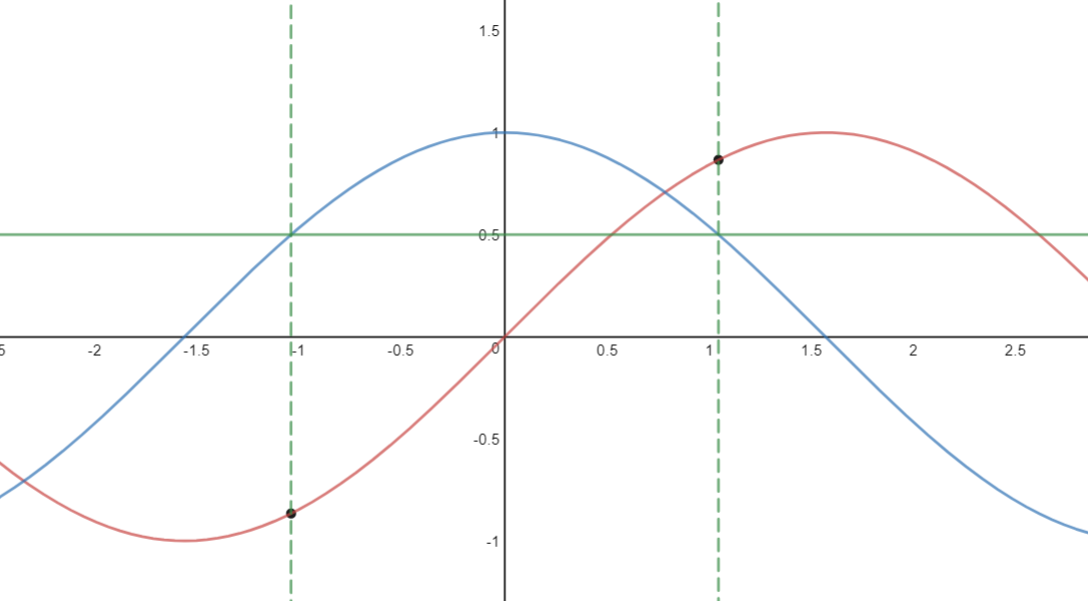
这样传统的神经网络就无法解决这类函数问题了，而 RNN 之所以能解决，是因为 RNN 知道 cos(x) 的值的时候，会根据先前的 cos(x) 的值，判断在当前点上升或者下降的趋势（递增递减），进而推断出 sin(x) 的值。当然这只是拟人的说法，本质还是 RNN 解决了依赖关系。

如果硬让普通神经网络解决这个问题呢？

file

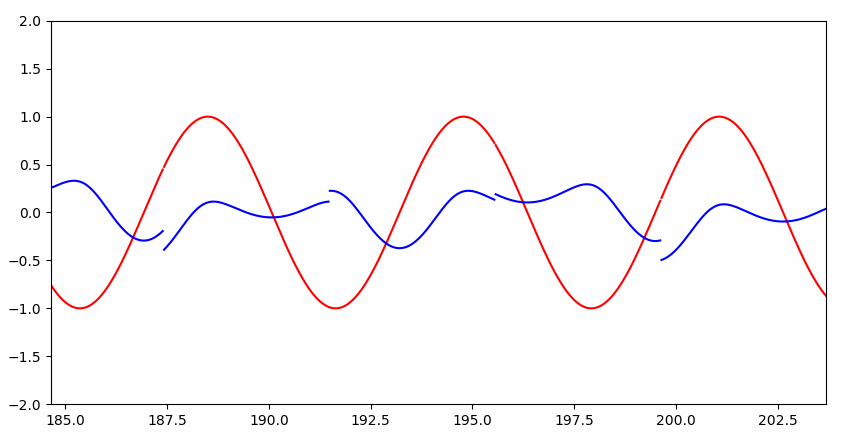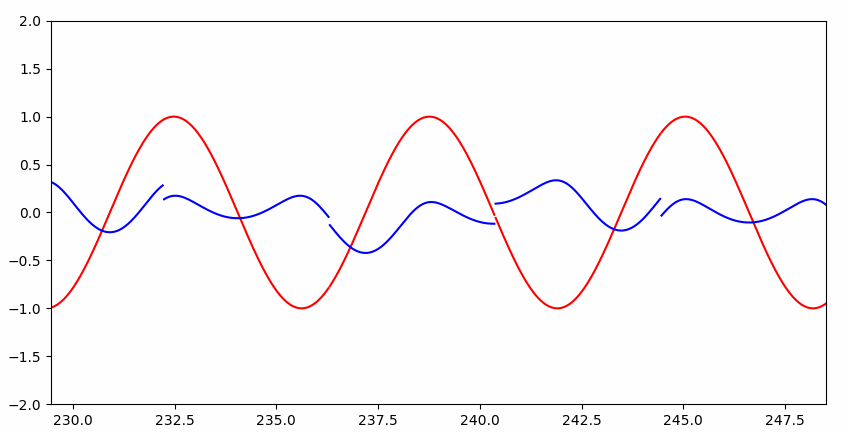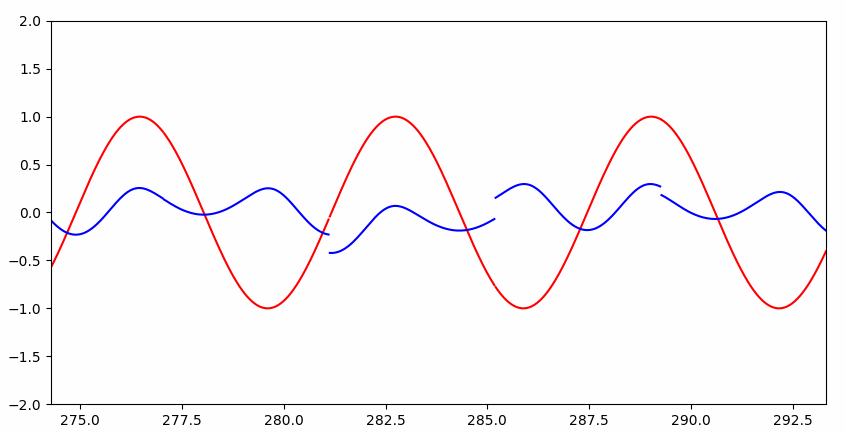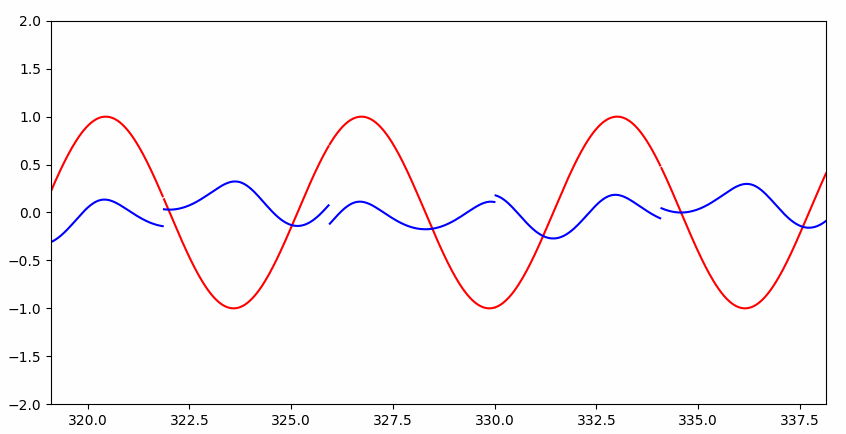
Interesting~~

参考

凡是讲到与 RNN 有关的问题，99.9% 的文章都要引用这两篇：

Understanding LSTM Networks （本篇也提到了链接2）
The Unreasonable Effectiveness of Recurrent Neural Networks

所以，还不赶紧去看这两篇文章？还有一个系列：Recurrent Neural Networks Tutorial, Part 1 – Introduction to RNNs 也超级棒。